Def:Se numeşte graf neorientat notat cu G o pereche ordonată de mulţimi G=(X,U),unde X este o mulţime finită şi nevidă de elemente,iar U este o mulţime de perechi formată din elemente distincte ale mulţimii X.
Def: G=(X,U)
X-este mulţimea nodurilor unui graf.
U- reprezintă mulţimea muchiilor unui graf.
Orice muchie este reprezentată printr-o pereche de noduri care reprezintă extremităţile unei muchii.Nodurile care reprezintă extremităţile aceleiaşi muchii se numesc adiacente,iar muchia este incidentă cu fiecare din nodurile ei.
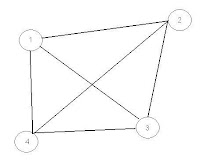
Reprezentarea grafica a unui graf cu n noduri:
n=4
X={1,2,3,4}
U={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}
In memoria calculatorului un graf neorientat
se reprezintă cu ajutorul matricii de adiacenţă,
Notată cu A(i,j).
A(i,j)=
A=0111
1011
1101
1110
Gradul unui nod reprezintă numărul muchilor incidente în nodul respectiv,se notează cu d(x).
d(1)=3
d(2)=3
d(3)=3
d(4)=3
Gradul unui nod neorientat este egal cu 2*m adică de doua ori numărul muchiilor.
Se numeşte nod terminal un nod care are gradul 1.
Se numeşte nod izolat un nod care are gradul 0.
Se numeşte nod intermediar un nod care are gradul mai mare ca 1.
TEOREME :
1.Numărul total de grafuri neorientate cu n noduri este 2^C^n^2.
2.Suma gradelor tuturor nodurilor unui graf neorientat este egala cu dublul numărului de muchii.
3.Dacă graful G neorientat are n noduri,n>2,atunci cel putin 2 noduri au acelasi grad.
4.Pentru orice graf neorientat numărul nodurilor de grad impar este par.
5.Numărul minim de muchii pe care trebuie să le aibă un graf neorientat cu n noduri,ca sa nu existe noduri izolate este[n+1/2].
Se numeşte lanţ într-un graf neorientat o succesiune de vîrfuri cu proprietatea că intre oricare două vîrfuri (noduri) există o muchie.Lungimea unui lanţ etse egală cu numărul de muchii sau cu numărul de noduri minus unu.
Numim lanţ elementar o succesiune de vîrfuri care respectă proprietatea de lanţ şi în care oricare 2 vîrfuri sunt distincte,în caz contrar lanţul se numeşte neelementar.
Se numeşte lanţ simplu o succesiune de varfuri cu proprietatea că fiecare muchie este vizitată o singură dată.
Se numeşte lanţ compus un lanţ în care o muchie este vizitată de cel puţin două ori.
Se numeşte ciclu intr-un lanţ neorientat o succesiune de varfuri cu proprietatea că primul nod coincide cu ultimul nod.
Grafuri derivate dintr-un graf
Se numeşte graf parţial notat cu proprietatea că mulţimea V de perechi de vîrfuri este inclusă un mulţimea U.
Se numeşte subgraf al unui graf G un graf cu proprietatea că mulţimea vîrfurilor Y este inclusă în mulţimea varfurilor X(Y<=X).Mulţimea perechilor V este inclusă in perechea U(V<=U).Mulţimea V este formată din valori distincte ale mulţimii Y.
Graful Nul
Graful nul este graful care are mulţimea U mulţime vidă(nu are muchii).
Graful Complet
Graful complet cu n noduri este un graf în care între oricare 2 noduri adiacente există o muchie.Într-un graf complet cu n noduri avem n(n+1)/2 muchii.
Graful Conex
Un graf se numeşte conex dacă între oricare 2 noduri ale sale găsim un lanţ care să le unească.
